go back

synapsium alpha build #3

6 January 2026

Full changelog

Level transitioning

Levels

New level: duality.
New level: trident.

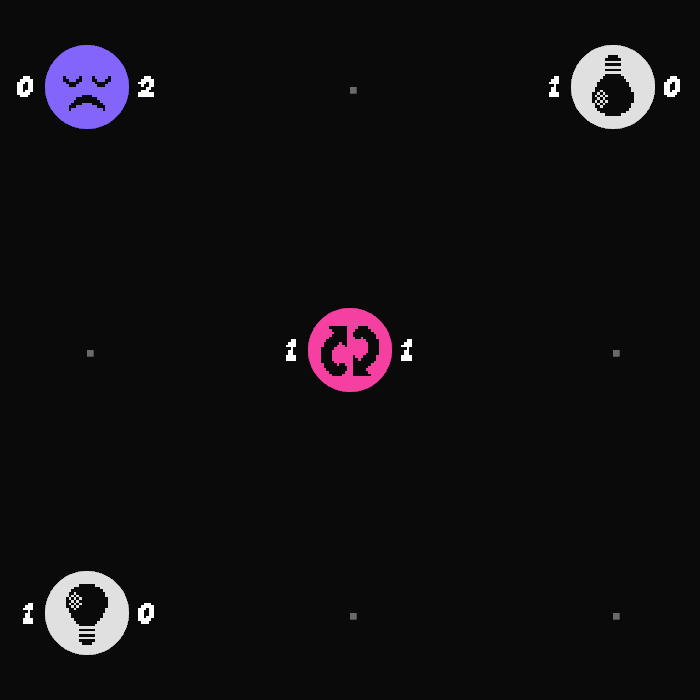
Colours

Nodes/particles

New network traversal logic

Introduction

I didn’t initially intend to overhaul the particle network traversal logic until I began playtesting the new level trident. I started with one goal in mind, which is perfectly encapsulated by the name of the GitHub branch: fix-rng. Little did I know, I was about to embark on quite the journey.

How the old system worked

Essentially, every particle has a source and a target. A particle is programmed to always travel from its current position towards its target. Its source is set to be the emitter from whence it came. Importantly, its source never changes (we want to always have a way to “send it back home”).

When a particle arrives at a node, it informs the node that it has arrived which triggers the node’s on_particle_arrived function. This function contains the node’s particle processing logic, but it also is responsible for informing the particle what its new target is.

How does it determine this new target? Well, each node has two lists of neighbours: _in_neighbours (for nodes which are inputs to the node) and _out_neighbours (for nodes which are outputs for the node). Under the old system, we simply selected a random neighbour from _out_neighbours to be the particle’s new target, thus allowing the particle to continue to flow through the network.

If, however, the particle reached a terminal node (i.e. a node with no _out_neighbours, such as a bulb), then we would set the particle’s target to be its source. This essentially sends the particle home to the emitter that created it.

Issues with the old system

There were two things that I didn’t like about the old system. The first was that it was possible for two particles to travel along the same edge (in the same direction). That is, if multiple particles reached a junction node (i.e. a node with more than one out-neighbour), say with out-neighbours A and B, then it was possible for the junction node to set the target of both particles to be A (25% chance). This didn’t feel very intuitive.

The second issue is related to the first. Let’s say that a particle arrives at a junction node with out-neighbours A, B, C, D, and E, all of which are terminal nodes with B a bulb. Moreover, B is the only bulb in the level, so it must be lit up (i.e. receive a particle) to complete the level.

Well, basic probability will tell you that there’s only a 20% chance that the particle takes the “right” path when arriving at the junction node, meaning that the player may have to sit and wait for the particle to take the correct path before the level can be completed. More disasterously, the player may get confused and think they have an incorrect solution when in actuality they don’t. This is a truly terrible consequence to occur in a puzzle game.

The second issue could be remedied by simply allowing more particles to flow through the network (this increases the probability that a particle takes the “right” path), though this wouldn’t solve the first issue.

Solving the first issue

The first issue was relatively easy to solve. I approached it by giving each node a counter called particles_targeting_this.

When a node, say A, sets a particle’s target to be another node, say B, then B’s particles_targeting_this counter is incremented. This essentially means that each node is now aware of how many particles are trying to arrive at it. Furthermore, whenever a particle arrives at a node, it decrements the node’s particles_targeting_this counter.

Now, when node’s choose what a particle’s target is going to be, instead of selecting an out-neighbour at random, they instead select the first available out-neighbour with a particles_targeting_this counter equal to 0. If no out-neighbours satisfy this condition, then we revert to the old system and choose a random out-neighbour.

This approach solves the first issue. That is, it means that it’s impossible for two particles to travel along the same connection in the same direction.

How attempting to solve the second issue introduced a more difficult third issue

With the first issue solved, I thought that simply introducing more particles into the network would solve the second issue and make everything run smoothly. Now, whilst this was true for all of the earlier levels, there was a problem waiting for me when trying to complete my new level trident (see the video below).

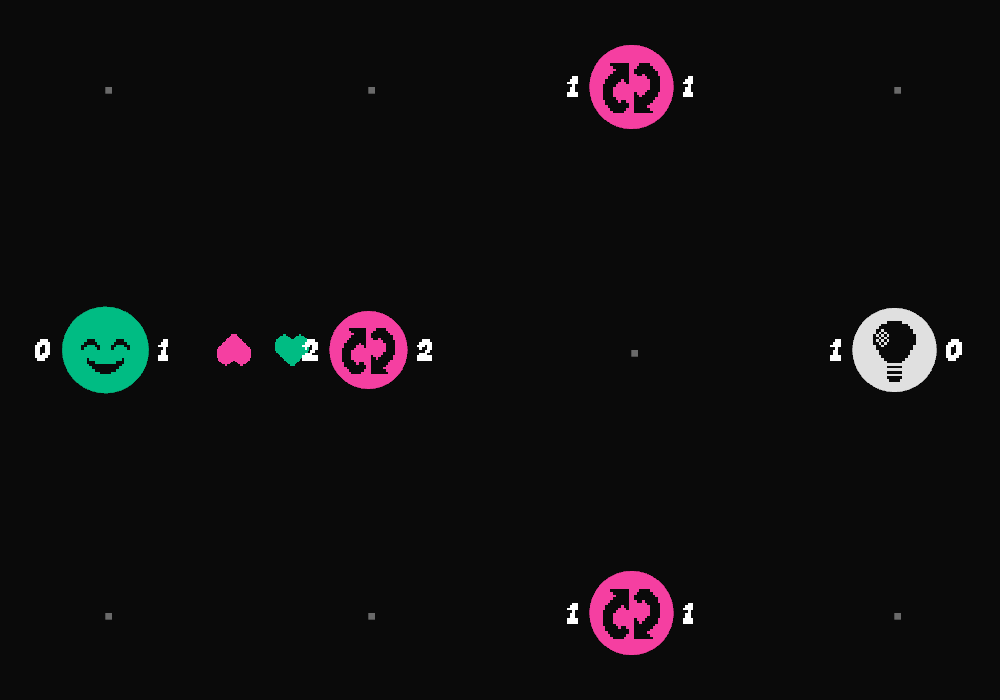
In the attached video, you can can see my new level trident. This is distinctly different from the previous levels since you can form a 3-cycle. Given that I’d solved the first issue, I thought that introducing two particles into this level would cause the 3-cycle to be a non-problem. However, I was very wrong.

Essentially, the three inverter nodes (the pink ones) form a 3-cycle and the leftmost one is connected to the bulb. However, you’ll notice in the video that whenever the particles arrive at the leftmost inverter, they never travel along the connection towards the bulb. This means that it’s impossible to complete the level (quite a problem).

Why does this happen? Well, when a particle arrives at the topmost inverter, it decrements its particles_targeting_this counter, and when a particle arrives at the leftmost inverter, it increments the topmost inverter’s particles_target_this counter. Since one particle always arrives at the topmost inverter before the other particle arrives at the leftmost inverter, the topmost inverter’s particles_target_this counter is always 0. This means that the topmost inverter is always chosen as the target for a particle when it arrives at the leftmost inverter. Thus, the particles travel around the 3-cycle indefinitely and neither of them ever end up at the bulb.

Fixing this new problem

I considered a few different options for solving the cycle problem. Initially, I experimented with adjusting how particles obtain their speed.

For a while now it has been the case that all particles have the same speed. I started toying around with a new paradigm: Relating a particle’s speed to the distance between its current position and its target. This means that if a particle is further away from its target, then it moves faster. This ended up being a cool feature that, once I tweak it a little bit and properly implement acceleration, I think I’ll keep, but it doesn’t really solve the cycle problem.

I also experimented with emitters increasing the speed of each successive particle that it releases. This meant that the last particle that the emitter emitted would be the fastest. In particular, it would be faster than all the previously emitted particles. However, this wasn’t really solving the problem. If anything, it was an inconsistent hacky solution.

Eventually, I came to my senses and correctly identified the source of the problem: Particles need to know whether they are in a cycle or not.

To do this, I gave each node a unique ID and each particle a std::unordered_set which was, over time, updated to contain the IDs of the nodes that it had visited. If insertion of an ID failed, then the particle must have already visited the node with that ID. That is, it knew that it was in a cycle.

Using this ID system, when a particle arrives at a node we can check whether it has visited the node before. If it has, then we can look through the node’s out-neighbours and attempt to find one that it hasn’t visited. If we find one, we set the particle’s target to that unvisited out-neighbour. If we can’t find one, then we fall back to the previous logic.

There are some other subtle nuances to this approach. In particular: When exactly should a particle’s stored IDs be cleared? If they are never cleared, then when the particle does a second pass through the network it will always think that it is in a cycle (since it has visited all of the nodes before). However, I’ll leave this question for the reader to ponder.

The final result

Revisiting the previously broken level trident with the new system in place, you can now see that the particles will only complete one loop of the inverter 3-cycle before going to the bulb. Thus, the level is completable again (yay).

What’s the point of all this?

This is a very valid question. Well, as I continue to expand this game, I’m going to be adding larger, more complex levels. Making sure that the particles flow through the network in a consistent, intuitive manner is paramount. After all, I don’t want the player to get confused about why something is happening.

My design philosophy thus far has been as follows: The nodes and the particles should only know as little information as possible. For example, the nodes don’t even know what type of node they’re connected to (i.e. whether it’s a bulb, emitter, et cetera). They are only aware that they are connected to another node.

With these changes to the traversal logic, both the nodes and the particles have a little bit more information about the network. This will hopefully be helpful moving forward.

Closing remarks

If you made it this far, thanks for reading. I’ll be back with another update on January 13th. Until then, peace and love.

Footnotes

  1. Previously they were entirely black to match the old background colour, meaning that they couldn’t be tinted to become a different colour. ↩

  2. Particles are programmed to always move towards their target. It notifies its target that it has arrived if the distance between it and its target is less than this distance threshold. ↩

  3. When the player moves a node, the node’s position linearly interpolates towards the mouse’s position. This means that it’s possible to drag a node whilst said node is not currently underneath the mouse. ↩